Welcome to the geometry section of our comprehensive ParaPro Study Guide. Geometry is a foundational branch of mathematics that you must be familiar with to succeed on the official ParaPro Exam. Below, our study guide covers the most common geometrical shapes and the equations used to evaluate quantities, such as the area and perimeter, of those shapes.
Geometrical Shapes
We will first go over some basic geometrical definitions and shapes.
- Perimeter: The sum of a 2D shape’s side lengths.
- Area: The amount of space within a 2D shape. The area will be represented as unit\(^2\).
- Volume: The amount of space occupied by a 3D shape. The volume will be represented as unit\(^3\).
- Diameter (\(\,d \,\)): A line segment that passes through the center and has 2 endpoints on the edge of the circle. It is twice the radius.
- Radius (\(\,r \,\)): Any segment from the center of a circle to its edge. It is half of the diameter.
- Circumference: The perimeter of a circle.
Square
A square has four equal sides. All of the sides are at right angles to each other.
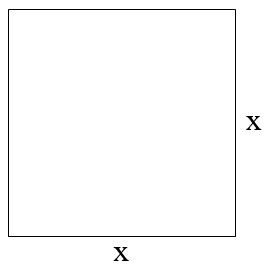
Perimeter = \(4x\)
Area \(= x^2\)
Rectangle
A rectangle has sides that are equal to their opposites. All of the sides are at right angles to each other.
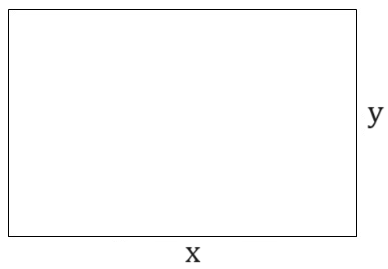
Perimeter = $2x + 2y$
Area = $xy$
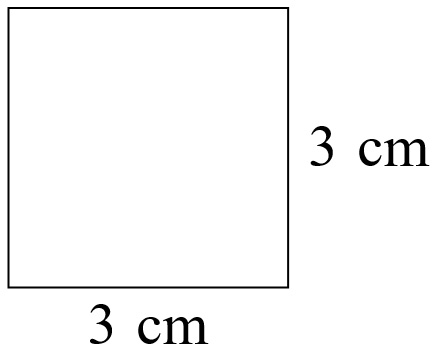
Example 1
Find the area and perimeter of the rectangle.
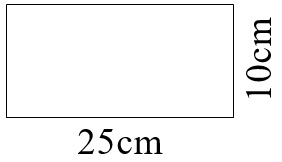
Area \( = \) length \( \times \) width \( = 25 × 10 = 250\) cm\(^2\)
Perimeter \(= 25 + 10 + 25 + 10 = 70\) cm
Circle
A circle has a fixed distance (the radius) from a fixed point (the center).
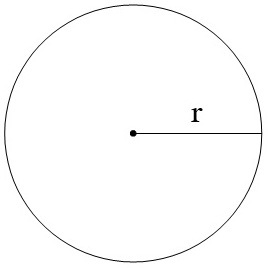
Circumference: \(πd \; (\text{or } 2πr)\)
Area \(= πr^2\)
Example 2
Find the area and circumference of the circle.
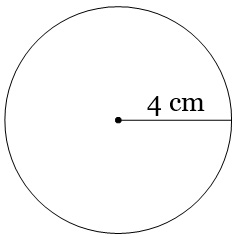
Area \( = π(4)^2 = 16 \ π\) cm\(^2\)
Diameter \(= 2 × 4 = 8 \) cm
⇒ Circumference \(= 8 \ π\) cm
Example 3
Find the diameter of a basketball hoop that has a circumference of 56.54 inches.
(Use $π = 3.14$)
Circumference \(= 3.14 \ \times \) diameter
\(⇒ 56.54 = 3.14 \ \times \) diameter
\(⇒ \dfrac{56.54}{3.14} = 18\) inches
Example 4
The circumference of a circle is 16π inches. What is the area of the circle?
Step 1: Use the formula for the circumference of the circle to find the radius of the circle.
\(C = 2πr\)
\(⇒ 16π = 2πr\)
\(⇒ \dfrac{16π}{2π} = r\)
\(⇒ 8 = r\)
Step 2: Find the area of the circle.
Area \(= πr^2\)
\(⇒\) Area \( = π(8)^2\)
\(⇒\) Area \(= π64\)
\(⇒\) Area \(= 64π\) inches\(^2\)
Parallelogram
A parallelogram has two parallel sets of sides, but its corners do not have to be at right angles. Thus, squares and rectangles are technically parallelograms, but not all parallelograms are squares or rectangles, such as in the example below.
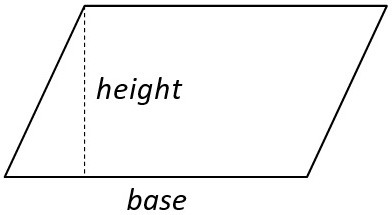
Area \(= base × height\)
Example 5
Find the height of a parallelogram that has an area of 52 units\(^2\) and a base of 13 units.
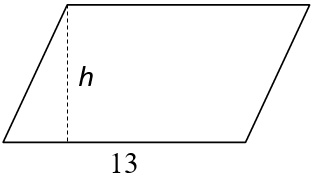
Area of a parallelogram = base × height
\(⇒ 52 = 13\) × height
Height \(= \dfrac{52}{13} = 4\)
The height of the parallelogram is \(4\) units.
Triangle
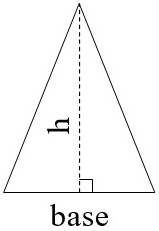
Area \(= \dfrac{1}{2}\) × base × height
Triangles, of course, are shapes with three sides. The same area formula is used for all triangles, but there are a few specific kinds of triangles that we’ve highlighted below.
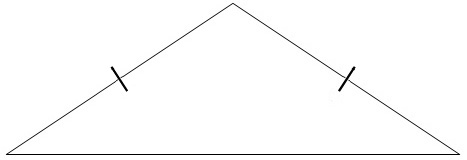
Isosceles Triangle
This triangle has two congruent sides, meaning they are the same length. They are often marked with a straight line on the congruent sides.
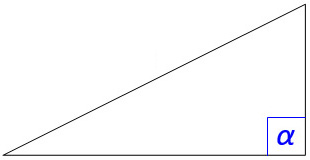
Right Triangle
Right triangles have one right angle, which is usually shown with a square to indicate 90°.
Polygon
Polygons are closed 2D shapes that have three or more sides.
3-sided polygons are triangles and 4-sided polygons are quadrilaterals. The table below lists a few polygons.
| 5 sides | Pentagon |
| 6 sides | Hexagon |
| 7 sides | Heptagon |
| 8 sides | Octagon |
A polygon can be classified as regular or irregular, depending on the length of its sides.
If all sides are of equal length, it is known as a regular polygon. For example, a triangle with all equal sides would be regular, and it would also be known as an equilateral triangle.
If all sides are not of equal length, it is known as an irregular polygon. For example, a triangle with all different sides would be irregular, and it would also be known as a scalene triangle.
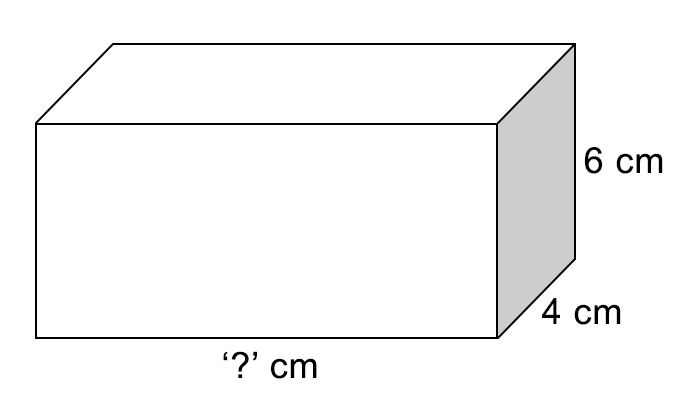
Cubes and Cuboids
Cubes are 3D shapes where all three sides (length, width, and height) are equal and opposite faces are parallel.
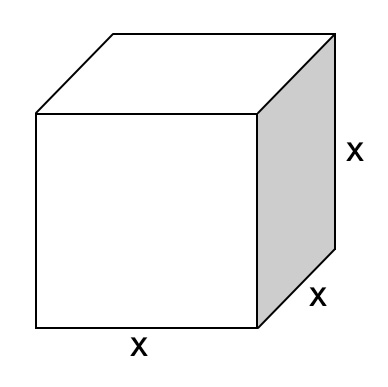
Volume \(= x^3\)
Cuboids are 3D shapes that have three sides of various lengths (which may or may not be equal) and opposite faces parallel.
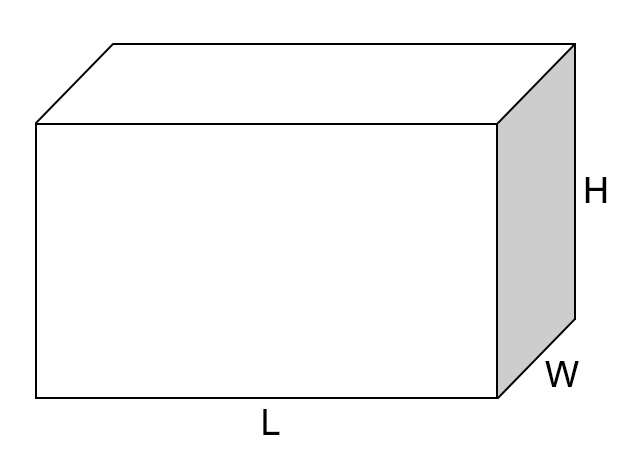
Volume \(= L × W × H\)
You should now be able to solve problems based on different geometric shapes. To test your knowledge and ability to apply it on the official ParaPro Exam, use our quick, 6-question geometry review test below.