Try our free ParaPro Math practice test. The math section consists of 30 multiple choice questions on basic math, algebra, geometry, measurement, and data analysis. Our online practice questions include answers and detailed explanations. You may not use a calculator on the ParaPro Math test.
Time limit: 0
Quiz Summary
0 of 30 Questions completed
Questions:
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You must first complete the following:
Results
Test complete. Results are being recorded.
Results
0 of 30 Questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 point(s), (0)
Earned Point(s): 0 of 0, (0)
0 Essay(s) Pending (Possible Point(s): 0)
Categories
- Not categorized 0%
-
Question 1 of 30
1. Question
A farmer has a rectangular field that measures 125 feet by 200 feet. He wants to enclose the field with a fence. What is the total length of fencing, in feet, that he will need for the job?
CorrectIncorrect -
Question 2 of 30
2. Question
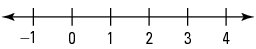
On the number line above, where is the number $\frac{7}{3}$ located?
CorrectIncorrect -
Question 3 of 30
3. Question
Tavon’s flight is 270 minutes long. How many hours does the flight last?
CorrectIncorrect -
Question 4 of 30
4. Question
In a factory, there are two separate containers of stress balls. In the first container are 80 balls, and in the second are 90 balls. 40% of the balls in the first container are defective, and 20% in the second container are defective. In total, how many balls in the two containers are defective?
CorrectIncorrect -
Question 5 of 30
5. Question
Ayana wants to buy as many bags of mulch as possible with her \$305, and she would like them to be delivered to her house. The cost is \$8.00 per bag and there is a \$21.00 delivery charge. The mulch is only sold in full bags. How many bags can Ayana buy?
CorrectIncorrect -
Question 6 of 30
6. Question
A family ordered $2$ large pizzas for lunch. They ate $\frac{7}{8}$ of one pizza and $\frac{1}{4}$ of the other pizza. How much pizza was left?
CorrectIncorrect -
Question 7 of 30
7. Question
Ryan buys a sweatshirt that costs \$50. A sales tax of 6% is added to the price. If Ryan gives three \$20 bills, how much change should he expect to receive?
CorrectIncorrect -
Question 8 of 30
8. Question
An equation and solution are shown below. One student asks for an explanation of how to arrive at that solution. Which explanation would be the best for the paraprofessional to provide?
Equation: $x + 17 = 11$
Solution: $x = −6$
CorrectIncorrect -
Question 9 of 30
9. Question
Tyler struggled with his math class early in the year, but he has been working hard to improve his scores. There is one test left, and he is hoping that his final average test score will be 75. What score will Tyler need to get on Test 6 to finish the year with an average score of 75?
Test Score Test 1 50 Test 2 52 Test 3 77 Test 4 88 Test 5 91 Test 6 CorrectIncorrect -
Question 10 of 30
10. Question
What is the solution to the following equation?
$8.77 − 10.16 =$
CorrectIncorrect -
Question 11 of 30
11. Question
Jodi buys nine pens at \$1.10 per pen. Which of the following represents the change she would receive if she purchased the pens using a \$20 bill?
CorrectIncorrect -
Question 12 of 30
12. Question
Hotdogs are sold in packs of 8. Bob buys five packs of hotdogs. If buns are sold in packs of 6, what is the least number of packs Bob can buy and still have enough buns for the hotdogs?
CorrectIncorrect -
Question 13 of 30
13. Question
The area of the circle shown below is $100π$. What is the diameter (D) of the circle?
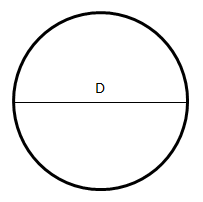 CorrectIncorrect
CorrectIncorrect -
Question 14 of 30
14. Question
Find the greatest common factor of $33$ and $44$.
CorrectIncorrect -
Question 15 of 30
15. Question
Arrange the following fractions in order from least to greatest.
$\dfrac{7}{5}, \dfrac{15}{4}, \dfrac{3}{2}, \dfrac{11}{4}, \dfrac{13}{3}$
CorrectIncorrect -
Question 16 of 30
16. Question
Devon owns a house cleaning company and has to give price quotes to potential customers. He figures out his price by assuming a $\$25$ base charge and then adding $\$8$ for each bathroom and $\$4$ for each other room. If he uses $P$ to represent the price, $B$ for bathrooms, and $R$ for other rooms, which of the following represents his price quote formula?
CorrectIncorrect -
Question 17 of 30
17. Question
Rose’s circular archery target has an area of 400$π$ square inches. What is the diameter of her target?
CorrectIncorrect -
Question 18 of 30
18. Question
Which of the following numbers is the greatest?
$\dfrac{2}{3}$, $0.6$, $\dfrac{13}{22}$, $0.08$
CorrectIncorrect -
Question 19 of 30
19. Question
Which of the following fractions is greater than 0.4 and less than 0.5?
CorrectIncorrect -
Question 20 of 30
20. Question
Coach Douglas is getting ready for another soccer season. He purchased 20 cones for \$1.25 per cone, 3 balls for \$25 per ball, and 12 practice vests for \$3.50 per vest. How much did the coach spend in total on the items?
CorrectIncorrect -
Question 21 of 30
21. Question
What is the value of the expression given below?
$26 − 7(3 + 5) ÷ 4 + 2$
CorrectIncorrect -
Question 22 of 30
22. Question
$5^3 × 8^2 =$
CorrectIncorrect -
Question 23 of 30
23. Question
Which of the following is the BEST estimate of 3995 × 102?
CorrectIncorrect -
Question 24 of 30
24. Question
One can of paint will cover 200 square feet. How many cans of paint will be needed to paint a large rectangular wall that is 66 feet long and 18 feet tall?
CorrectIncorrect -
Question 25 of 30
25. Question
A student is calculating the average of a list of seven numbers. After adding the seven numbers together, he accidentally multiplied by 7 instead of dividing and got 392. Which of the following could the ParaProfessional have the student do to get the correct average without having to clear the calculator and start over?
CorrectIncorrect -
Question 26 of 30
26. Question
At a used book store, Valentina purchased three books for $\$2.65$ each. If she paid with a $\$20$ bill, how much change did she receive?
CorrectIncorrect -
Question 27 of 30
27. Question
$6 × (15 − 8) − (3 − 10)$
The correct solution to the above problem is $49$. What would be the correct solution if both pairs of parentheses were removed?
CorrectIncorrect -
Question 28 of 30
28. Question
Emma, Olivia, Ava, and Amelia were left an inheritance by their grandmother. If Emma receives one-eighth of the inheritance, Olivia receives one-quarter of the inheritance, Ava receives three-eighths of the inheritance, and Amelia receives the remainder, what fraction of the inheritance does Amelia receive?
CorrectIncorrect -
Question 29 of 30
29. Question
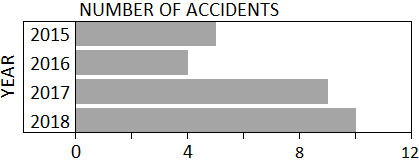
The number of accidents occurring at a dangerous intersection is shown in the chart above. What is the average number of accidents per year during the four years shown (2015–2018)?
CorrectIncorrect -
Question 30 of 30
30. Question
If you first add 4 to Kaden’s age and then multiply this sum by 3, you will have his father’s age of 51 years old. Which of the following properly represents this statement algebraically?
CorrectIncorrect
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- Current
- Correct
- Incorrect
