In this section of our ParaPro Study Guide, we will see what variables, expressions, and equations are. We will go also through the steps of solving one-step linear equations and discuss coordinate planes and cartesian coordinates.
What are Variables, Expressions, and Equations?
A variable is a letter that is used to represent a number whose value is unknown. Examples of variables are $a, b, c,$ or $x$.
Variables can be added, subtracted, multiplied, and divided with numbers to form expressions. For example, $10x$ shows a number multiplied by $10$, and $y + 8$ shows a number added to $8$.
When an expression is equal to a number, we call it an equation. This is shown using the “equal to” sign, “$=$.” For example, $x + 8 = 12$.
How to Solve One-Step Linear Equations
To solve a linear equation means to find the value of the variable that would make the equation true.
To solve a linear equation, you should isolate the variable. To isolate the variable, you use inverse operations, which means you perform the opposite action of the symbol shown (the opposite of addition is subtraction, the opposite of multiplication is division, and so on).
Whatever inverse operation you do to the left side, you need to do the same on the right side for the equality to hold true.
Example 1
Solve: $x + 5 = 12$
To isolate the variable $(x)$, you undo adding $5$ by subtracting $5$ from both sides of the equation.
$x + 5 \ – \ 5 = 12 \ – \ 5 \ \ → \ \ x = 7$
Example 2
Solve: $b \ – 19 = 20$
To isolate the variable $(b)$, you undo subtracting $19$ by adding $19$ to both sides of the equation.
$b \ – 19 + 19 = 20 + 19 \ \ → \ \ b = 39$
Example 3
Solve: $3k = 24$
To isolate the variable $(k)$, you undo multiplying by $3$ by dividing both sides of the equation by $3$.
$ \dfrac{3k}{3} = \dfrac{24}{3} \ \ → \ \ k = 8$
Example 4
Solve: $ \dfrac{x}{4} = 16$
To isolate the variable $(x)$, you undo dividing by $4$ by multiplying both sides of the equation by $4$.
$4 × \dfrac{x}{4} = 16×4\ \ → \ \ x = 64$
Example 5
The three lengths of an irregular quadrilateral are $4, 8,$ and $5$. If the perimeter of the quadrilateral is $23$, write an equation for the missing length.
Represent the missing length with $l$.
The perimeter of a quadrilateral is equal to the sum of all its lengths:
Sum $= l+4+8+5 = l+17$
Since this is equal to $23$, the equation is $l+17=23$.
Coordinate Planes
The coordinate plane is the space created by the $x$-axis (horizontal axis) and the $y$-axis (vertical axis).
The center of the coordinate plane is known as the origin, $(0,0)$.
To locate a point on the coordinate plane, the coordinate pair $(x,y)$ indicates how far to move left or right $(x)$ and up or down $(y)$ from the origin.
Example 6
Plot the coordinates $(2,4)$ on the coordinate plane.
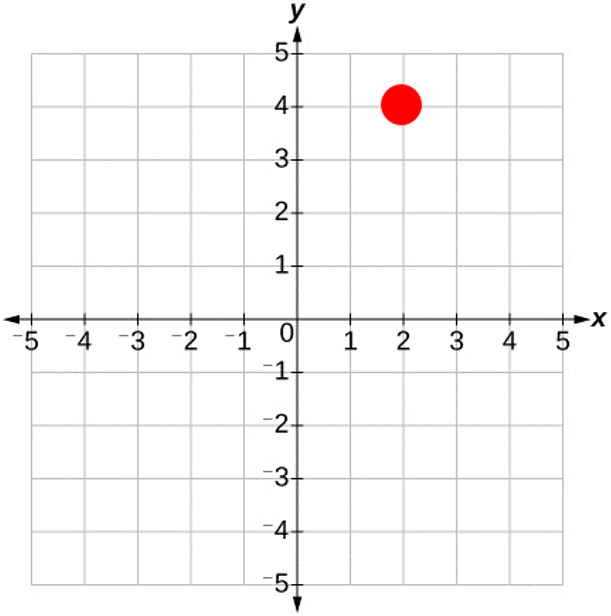
The point $(2,4)$ is located by going $2$ units to the right and $4$ units up from the origin.
Example 7
Plot the coordinates $(-3,-1)$ on the coordinate plane.
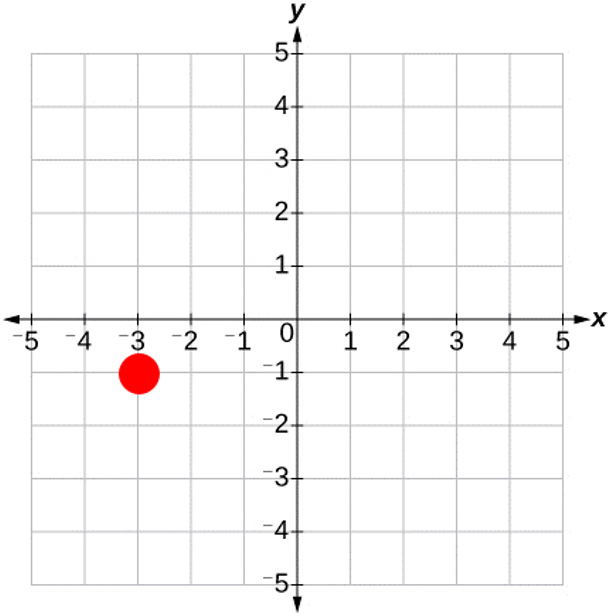
The point $(-3,-1)$ is located by going $3$ units to the left and $1$ unit down from the origin.
Now you should have a better hand on how and why variables are used, how to solve for them in linear equations, and how to work with a coordinate plane. Check your understanding of all of the above with our six-question review test below.