This page of our free ParaPro Study Guide covers fractions. It starts by describing the basics of fractions and then moves on to adding, subtracting, multiplying, and dividing fractions. Finally, it shows how to compare fractions.
What is a Fraction?
A fraction is made of two numbers: the numerator on the top and the denominator on the bottom.
$\dfrac{\text{Numerator}}{\text{Denominator}}$
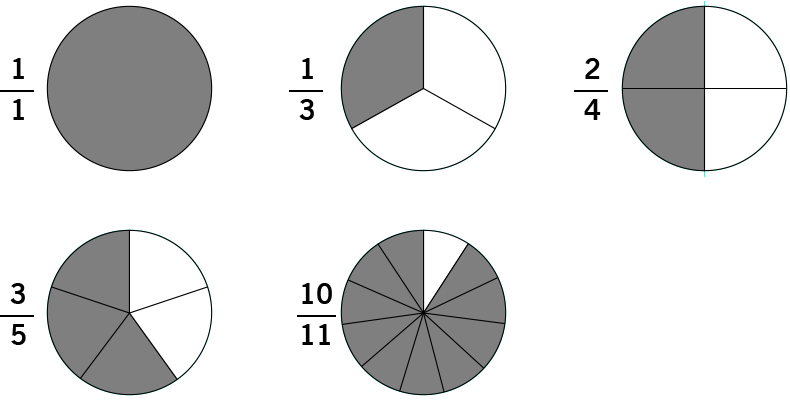
The numerator is the number of parts we have considered and the denominator is the number of parts we divide the whole into. In the pictures below, the numerator represents how many pieces are shaded out of the whole (the denominator). For example, $\frac{1}{3}$ represents $1$ shaded piece out of $3$ total pieces.
Adding and Subtracting Fractions
To add/subtract fractions with the same denominator, simply add/subtract the numbers in the numerator. The denominator stays the same.
Example 1
Example 2
\(⇒\) We can write \(\dfrac{3}{6}\) as \(\dfrac{1}{2}\) since the two fractions are equivalent.
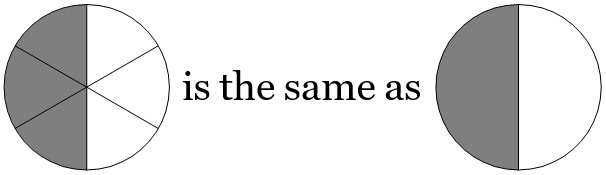
Equivalent Fractions
To find an equivalent fraction, multiply the numerator and the denominator by the same number. For example, when $\frac{1}{8}$ is multiplied by $4$ in the numerator and the denominator, we get $\frac{4}{32}$. Thus, $\frac{1}{8}$ and $\frac{4}{32}$ are equivalent fractions.
Note: When we divide the numerator and the denominator as many times as possible to find an equivalent fraction with the smallest possible numbers, we call it reducing the fraction.
Example 3
To add/subtract fractions with different denominators, we have to make the denominators the same. To do this, we can find the least common multiple, or the smallest number that both denominators can multiply to. Take the following fractions as an example:
$\dfrac{1}{7}$ and $\dfrac{9}{14}$
The lowest common multiple of $7$ and $14$ is $14$. Thus, each denominator can be multiplied by another number to equal $14$ ($7 \times 2$ and $14 \times 1$). Thus, we can multiply the first fraction by $\frac{2}{2}$ and the second by $\frac{1}{1}$ to get equivalent fractions that can be added and subtracted.
If you aren’t sure of the least common multiple of two numbers, you can always arrive at a common multiple by multiplying each fraction by the denominator of the other. It might not be the smallest number you can work with, but it will still work out:
\(\dfrac{a}{b} + \dfrac{c}{d} \) \( = \dfrac{a \times d}{b \times d} + \dfrac{c \times b}{d \times b} \) \( = \dfrac{ad + bc}{bd}\)
Example 4
\(\dfrac{2 \times 4}{3 \times 4} + \dfrac{1 \times 3}{4 \times 3} \) \( = \dfrac{8}{12} + \dfrac{3}{12} \) \( = \dfrac{8+3}{12} = \dfrac{11}{12}\)
Example 5
Sometimes, we subtract a fraction from a whole number. To do this, change the whole number \((1, 2, 3, …)\) into a fraction such that the denominator matches the fraction you are subtracting:
\( \dfrac{2}{2}, … \dfrac{4}{4}, … \dfrac{10}{10}, … \) are all equal to \(1\)
\( \dfrac{4}{2}, … \dfrac{8}{4}, … \dfrac{10}{5}, … \) are all equal to \(2\)
Example 6
Example 7
\(\dfrac{3}{1} + \dfrac{5}{6} = \dfrac{3 \times 6}{1 \times 6} + \dfrac{5}{6} \) \( = \dfrac{18+5}{6} = \dfrac{23}{6}\)
Multiplying Fractions
To multiply fractions, multiply the numerators and denominators straight across:
\( \dfrac{a}{b} \times \dfrac{c}{d} = \dfrac{a \times c}{b \times d}\)
When multiplying a whole number with a fraction, multiply the whole number with the numerator and keep the same denominator:
$ \# \times \dfrac{a}{b} = \dfrac{\# \times a}{b}$
Example 8
Example 9
Dividing Fractions
Dividing fractions uses the ”keep-change-flip” method:
\( \; \; \; \dfrac{a}{b} \qquad \; \div \qquad \dfrac{c}{d} \)
\(\; \; \; ↑ \ \qquad \; ↑ \ \qquad ↑\)\(Keep \quad change \quad flip\)
\(\; \; \;↓ \ \qquad \; ↓ \ \qquad ↓\)
\(\; \; \; \dfrac{a}{b} \; \qquad \times \qquad \dfrac{d}{c} \)
The first fraction stays the same, the division symbol changes to a multiplication symbol, and the second fraction is flipped. Essentially, we are turning a division problem into a multiplication one. You can also use a rhyming mnemonic to remember this rule: “When dividing fractions, don’t ask why, just flip the second and multiply!”
Example 10
\( \dfrac{3}{5} \div \dfrac{2}{7} = \; ?\)
\( \; \; \dfrac{3}{5} \qquad \qquad \div \qquad \qquad \ \dfrac{2}{7} \)
\(\; \; ↑ \qquad \qquad \ ↑ \qquad \qquad \ ↑\)
\(Keep \quad \qquad change \qquad \quad flip\)
\(\; \; ↓ \qquad \qquad \ ↓ \qquad \qquad \ ↓\)
\(\; \; \dfrac{3}{5} \qquad \qquad \times \qquad \qquad \ \dfrac{7}{2} \)
\( ⇒ \dfrac{3 \times 7}{5 \times 2} = \dfrac{21}{10}\)Comparing Fractions
We can compare fractions by finding a common denominator between the two fractions. This is similar to how we add or subtract fractions with different denominators: we first find a common denominator. We will use this same approach to compare fractions.
Some symbols we will be using to compare fractions:
- \(\lt\) less than
- \(\gt\) greater than
- \(\le\) less than or equal to
- \(\ge\) greater than or equal to
Example 11
Which of the following fractions is bigger?
\( \dfrac{2}{3} \text{ or } \dfrac{4}{5}\)
The first step is to make the denominators the same for both fractions by multiplying \( \dfrac{2}{3} \) by \(\dfrac{5}{5}\) and \( \dfrac{4}{5} \) by \(\dfrac{3}{3}\):
\(⇒ \dfrac{10}{15} \) O \( \dfrac{12}{15} \)
\(⇒\) Now, it is easy to compare these two fractions because we can look at the number in the numerator and see which is bigger.
\(⇒ \dfrac{10}{15} \lt \dfrac{12}{15} \)
\(\dfrac{4}{5}\) is the bigger fraction.
Example 12
Which of the following fractions is bigger?
\( \dfrac{3}{8} \text{ or } \dfrac{5}{12}\)
The first step is to make the denominators the same for both factions by multiplying \(\dfrac{3}{8}\) by \(\dfrac{3}{3}\) and \(\dfrac{5}{12}\) by \(\dfrac{2}{2}\):
\(⇒ \dfrac{3}{8} \times \dfrac{3}{3} \) O \( \dfrac{5}{12} \times \dfrac{2}{2}\)
\(⇒ \dfrac{9}{24} \) O \( \dfrac{10}{24}\)
\(⇒\) Since the denominators are now the same, we can compare the numbers in the numerator:
\(⇒ \dfrac{9}{24} \lt \dfrac{10}{24} \)
\(\dfrac{5}{12}\) is bigger.
Example 13
Sort the following fractions from smallest to largest:
\( \dfrac{2}{3}, \dfrac{5}{9}, \dfrac{16}{18}, \dfrac{5}{6} \)
The first step is to find a common denominator between all \(4\) fractions. Since \(18\) is the Least Common Denominator (smallest common multiple of \(3, 9, 6, 18\)), we multiply each fraction to make the denominator equal to \(18\):
\(⇒ \dfrac{2}{3} \times \dfrac{6}{6} = \dfrac{12}{18}\) \(⇒ \dfrac{5}{9} \times \dfrac{2}{2} = \dfrac{10}{18}\) \(⇒ \dfrac{16}{18}\) \(⇒ \dfrac{5}{6} \times \dfrac{3}{3} = \dfrac{15}{18} \) Since the denominators are now the same, we can write the numbers in the numerator from smallest to largest: \(10, 12, 15, 16\).The original fractions from smallest to largest:
\(⇒ \dfrac{5}{9}, \dfrac{2}{3}, \dfrac{5}{6}, \dfrac{16}{18}\)
At this point, you know a lot about fractions! You should be able to add, subtract, multiply, and divide them. Hopefully you reviewed all 13 examples and understand how to solve problems of this type. Before moving on to the next part of this study guide, be sure to try our fractions review test.
